|
Toroid
by Liliana Usvat
In mathematics, a toroid is a doughnut-shaped object, such as an O-ring. It is a ring form of a solenoid.
A toroid is used as an inductor in electronic circuits, especially at low frequencies where comparatively large inductances are necessary.
Torus
In geometry, a torus (pl. tori) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a ring torus or simply torus if the ring shape is implicit.
A torus can be defined parametrically by:
  
where
- θ, φ are angles which make a full circle, starting at 0 and ending at 2π, so that their values start and end at the same point,
- R is the distance from the center of the tube to the center of the torus,
- r is the radius of the tube.
R and r are also known as the "major radius" and "minor radius", respectively. The ratio of the two is known as the "aspect ratio". A doughnut has an aspect ratio of about 2 to 3.
An implicit equation in Cartesian coordinates for a torus radially symmetric about the z-axis is

or the solution of f(x, y, z) = 0, where

Algebraically eliminating the square root gives a quartic equation,

The three different classes of standard tori correspond to the three possible relative sizes of r and R. When R > r, the surface will be the familiar ring torus. The case R = r corresponds to the horn torus, which in effect is a torus with no "hole". The case R < r describes the self-intersecting spindle torus. When R = 0, the torus degenerates to the sphere.
When R ≥ r, the interior

of this torus is diffeomorphic (and, hence, homeomorphic) to a product of an Euclidean open disc and a circle.
The surface area and interior volume of this torus are easily computed using Pappus's centroid theorem giving
 
These formulas are the same as for a cylinder of length 2πR and radius r, created by cutting the tube and unrolling it by straightening out the line running around the center of the tube. The losses in surface area and volume on the inner side of the tube exactly cancel out the gains on the outer side.
As a torus is the product of two circles, a modified version of the spherical coordinate system is sometimes used. In traditional spherical coordinates there are three measures, R, the distance from the center of the coordinate system, and θ and φ, angles measured from the center point. As a torus has, effectively, two center points, the centerpoints of the angles are moved; φ measures the same angle as it does in the spherical system, but is known as the "toroidal" direction. The center point of θ is moved to the center of r, and is known as the "poloidal" direction. These terms were first used in a discussion of the Earth's magnetic field, where "poloidal" was used to denote "the direction toward the poles".In modern use these terms are more commonly used to discuss magnetic confinement fusion devices.
n-dimensional torus
The torus has a generalization to higher dimensions, the n-dimensional torus, often called the n-torus or hypertorus for short. (This is one of two different meanings of the term "n-torus".) Recalling that the torus is the product space of two circles, the n-dimensional torus is the product of n circles. That is:

The 1-torus is just the circle: T1 = S1. The torus discussed above is the 2-torus, T2. And similar to the 2-torus, the n-torus, Tn can be described as a quotient of Rn under integral shifts in any coordinate. That is, the n-torus is Rn modulo the action of the integer lattice Zn (with the action being taken as vector addition). Equivalently, the n-torus is obtained from the n-dimensional hypercube by gluing the opposite faces together.
An n-torus in this sense is an example of an n-dimensional compact manifold. It is also an example of a compact abelian Lie group. This follows from the fact that the unit circle is a compact abelian Lie group (when identified with the unit complex numbers with multiplication). Group multiplication on the torus is then defined by coordinate-wise multiplication.
Toroidal groups play an important part in the theory of compact Lie groups. This is due in part to the fact that in any compact Lie group G one can always find a maximal torus; that is, a closed subgroup which is a torus of the largest possible dimension. Such maximal tori T have a controlling role to play in theory of connected G. Toroidal groups are examples of protori, which (like tori) are compact connected abelian groups, which are not required to be manifolds.
Magnetic Field of Toroid
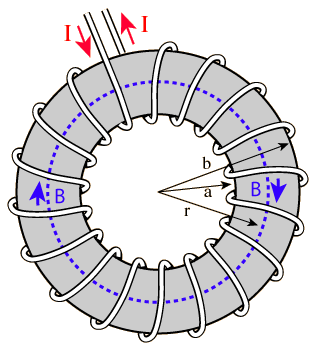
|
Finding the magnetic field inside a toroid is a good example of the power of Ampere's law. The current enclosed by the dashed line is just the number of loops times the current in each loop. Amperes law then gives the magnetic field by

The toroid is a useful device used in everything from tape heads to tokamaks. |
Free energy
There are dedicated independent scientists around the world that claim that we can generate unlimited clean energy by just tapping into the ‘torus’, a shape that supposedly pervades the universe, and which could yield endless free energy.
Toroid and Nature
The Sun has a large toroidal field surrounding it — the heliosphere — that is itself embedded inside a vastly larger toroidal field encompassing the Milky Way galaxy. Our Earth’s magnetic field is surrounding us and is inside the Sun’s field, buffering us from the direct impact of solar electromagnetic radiation. Earth’s atmosphere and ocean dynamics are toroidal and are influenced by the surrounding magnetic field. Ecosystems, plants, animals, etc all exhibit torus flow dynamics and reside within and are directly influenced by (and directly influence) the Earth’s atmospheric and oceanic systems. And on it goes inward into the ecosystems and organs of our bodies, the cells they’re made of, and the molecules, atoms and sub-atomic particles.
Continuing our exploration of the torus as a form and flow process, one of the key characteristics of it is that at its very center, the entire system comes to a point of ultimate balance and stillness — in other words, perfect centeredness.
Phylosophy
The torus is the oldest structure in existence and without it nothing could exist. The toroidal shape is similar to a donut but rather than having an empty central “hole”, the topology of a torus folds in upon itself and all points along its surface converge together into a zero-dimensional point at the center called the Vertex.
It has even been suggested that the torus can be used to define the workings of consciousness itself. In other words…consciousness has a geometry! The geometric shape used to describe the self-reflexive nature of consciousness is the torus. The torus allows a vortex of energy to form which bends back along itself and re-enters itself. It ‘inside-outs’, continuously flowing back into itself. Thus the energy of a torus is continually refreshing itself, continually influencing itself.
All Toroids have a black hole at one end and a white hole at the other. Black holes suck in energy and white holes emit it. So in our human body toroids we have black (negatively charged) and white (positively charged) holes.
When the torus is in balance and the energy is flowing we are in a perfect state to clear ourselves of anything that is ‘not self’ anything that prevents us being our authentic selves.
The infinity symbol an ancient two dimensional representation of the 3D double toroidal energy flow – self generating, continual, never ending.
Theorists in astrophysics now argue that each electron holds at its core “zero point energy,” as does the universe at large.
Zero point energy is a place where there is no sound or light. This nothingness, issuing the essence of everything, exists at the heart of creation. It is the place wherein miraculous manifestation from nothing to something happens.
|