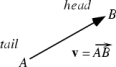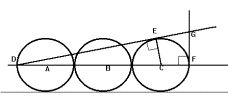|
|
||||||||||
| Mathematics Magazine for Grades 1-12 |
||||||||||
|
|
||||||||||
|
|
||||||||||
Theory:
Vector
A vector is formally defined as an element of a vector
space. In the commonly encountered vector space
Vectors can be added together (vector addition), subtracted
(vector subtraction) and multiplied by scalars (scalar multiplication). Vector
multiplication is not uniquely defined, but a number of different types of
products, such as the dot product, cross product, and tensor direct product can
be defined for pairs of vectors. A vector from a point A to a point B is
denoted
giving
A zero vector, denoted 0, is a vector of length 0, and thus has all components equal to zero. Since vectors remain unchanged under translation, it is often convenient to consider the tail A as located at the origin when, for example, defining vector addition and scalar multiplication. A vector may also be defined as a set of n numbers Aa, ..., An that transform according to the rule
where Einstein summation notation has been used,
are constants (corresponding to the direction cosines),
with partial derivatives taken with respect to the original and transformed
coordinate axes, and i, j=1, ..., n (Arfken 1985, p. 10). This makes a vector a tensor of tensor rank one. A vector
with n components in called an n-vector, and a scalar may
therefore be thought of as a 1-vector (or a 0-tensor rank tensor). Vectors are
invariant under translation, and they reverse sign upon inversion. Objects that
resemble vectors but do not reverse sign upon inversion are known as
pseudovectors. To distinguish vectors from pseudovectors, the former are
sometimes called polar vectors. Solutions from the Previous Issue:
1.
Three circles with centers A, B and C are tangent to each other.
Each circle has radius 5. Lines DE and FG are tangent to C and intersect at G.
Find the length of FG.
Solution: We know < F to be 90 degrees (radius perpendicular to tangent) < CED 90 degrees delta DGF is similar to delta DCE by AAA
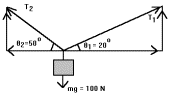
2. Write a system of equations and solve for T1 and T2.
Solution: mg = T1 sin θ1, + T2 sin θ2 100N = T1 sin 20o, + T2 sin 50 o T1 cos 20 o = T2 cos 50 o T1 = T2 cos 50 o / cos 20 o 100 N = T2 cos 50 o
100 N = T2 (cos 50 o sin 20 o + sin 50 o cos 20 o) / cos 20 o 100N (cos (20 o)) / sin 70 o = T2 T2 = 100 N T1 = 100 cos 50 o / cos 20 o = 68.4N 3.
An object released from rest at a position 20m above the ground is
governed by the following, equation: g = 9.81 m/s2, vo = 0
yo = 0
How long does it take the falling object to reach the ground? What speed does it travel at t = 1s? Solution: -20 = - 1/2 gt2 + 0 40/g = t2 t = 2.02s time to reach ground y = - 1/2 gt2 + yo = 0 At t = 1 v = -g (1) = -g = - 9.81 m/s Proposed Problems: 1. Given n > 2 points in the plane, prove that at most n pairs of points are the maximum distance apart (of any two points in the set). 2. The tetrahedron ABCD is divided into two parts by a plane parallel to AB and CD. The distance of the plane from AB is k times its distance from CD. Find the ratio of the volumes of the two parts. 3. The coefficients aij of the following equations a11x1 + a12
x2+ a13 x3 = 0 satisfy the following: (a) a11, a22, a33 are positive, (b) other aij are negative, (c) the sum of the coefficients in each equation is positive. Prove that the only solution is x1 = x2 = x3 = 0. |
||||||||||
|
Read more on the written version of the publication. |
||||||||||
(i.e.,
Euclidean n-space), a vector is given by n coordinates and can be
specified as (A1,A2,…An). Vectors are
sometimes referred to by the number of coordinates they have, so a 2-dimensional
vector (x1,x2) is often called a two-vector, an n-dimensional
vector is often called an n-vector, and so on.
, and a
vector v may be denoted
, or more
commonly, v. The point A is often called the "tail" of
the vector, and B is called the vector's "head." A vector with
unit length is called a unit vector and is denoted using a hat,
. An
arbitrary vector may be converted to a unit vector by dividing by its norm
(i.e., length),
